Door Marc van Oostendorp
De namen van getallen zijn opvallend traag. Dat is de conclusie van een nieuw onderzoek dat verscheen in Philosophical Transactions of the Royal Society B (Biology). De auteurs, beide evolutiebioloog, laten zien dat telwoorden (een, twee, drie, vier, enz.) minder snel veranderen dan andere woorden. In verwante talen lijken ze, gemiddeld genomen, meer op elkaar dan andere woorden: un, deux, trois, quattre, enz. staan dichter bij hun equivalenten in het Nederlands, dan laten we zeggen homme, main, arbre, dormir, ook al zijn die woorden ook al heel oud, en verwijzen ze sinds onheuglijke tijden naar alledaagse begrippen uit het leven van alle mensen.
Het geldt, blijkens het onderzoek, ook niet alleen voor Europese talen: ook in Bantoe-talen (zuidelijk Afrika) en Pama-Nyungan (Australië) bleken (rang)telwoorden (3,5 tot 20 keer) trager te veranderen dan andere woorden.
De auteurs bespreken ook drie mogelijke verklaringen voor dit verschil. De eerste is dat telwoorden al een kleine fonetische ruimte beslaan. Dat wil zeggen: ze zijn kort en aan korte woorden valt meestal niet zo veel te veranderen zonder dat ze te veel gaan lijken op een ander woord. Haal van drie de r weg, en je krijgt die, haal de d weg en je krijgt Rie. Verander de ie in een ee en je krijgt Dré. Lange woorden hebben meestal veel meer ruimte om te veranderen: van encyclopedie kun je zo’n beetje iedere medeklinker veranderen of weglaten zonder dat het op een woord begint te lijken. (Het is om die reden ook niet raadzaam om al te lange woorden te kiezen als je galgje speelt. Bij korte woorden komt het er veel meer op aan dat je iedere letter goed hebt.)
Paar
Dat kan een deel van de verklaring zijn, maar het verschuift het raadsel natuurlijk ook alleen maar: waarom zijn die telwoorden dan zo kort?
Ook een tweede verklaring geeft maar een deeltje van de puzzel: telwoorden hebben een veel preciezere, nauwer omschreven betekenis dan andere woorden. Twee, drie en dergelijke zijn allesbehalve vaag. Vage woorden hebben eerder de neiging aan de wandel te gaan: en zo kan het woord voor man ook het woord voor mens worden, of omgekeerd. En in ieder geval moet er iets aan de vorm veranderen om allebei de woorden uit elkaar te kunnen blijven houden.
Maar ook hier is uiteindelijk dan toch weer de vraag: waarom zijn we veel minder geneigd telwoorden metaforisch te gebruiken dan andere woorden? Waarom kan paar wel ‘een klein aantal’ betekenen, maar twee niet zo snel?
Kinderen
De derde verklaring ligt misschien het meest in de buurt, in die zin dat hij ook licht zou kunnen werpen op de andere twee: onze hersenen gaan op een andere manier om met telwoorden dan met andere woorden. De auteurs geven helaas niet zo veel bewijs voor die stelling als je zou willen – geen kaart van de hersenen met een pijltje ‘hier zitten de telwoorden’ – maar ze laten bijvoorbeeld wel zien dat kinderen telwoorden in een ander tempo leren: relatief snel.
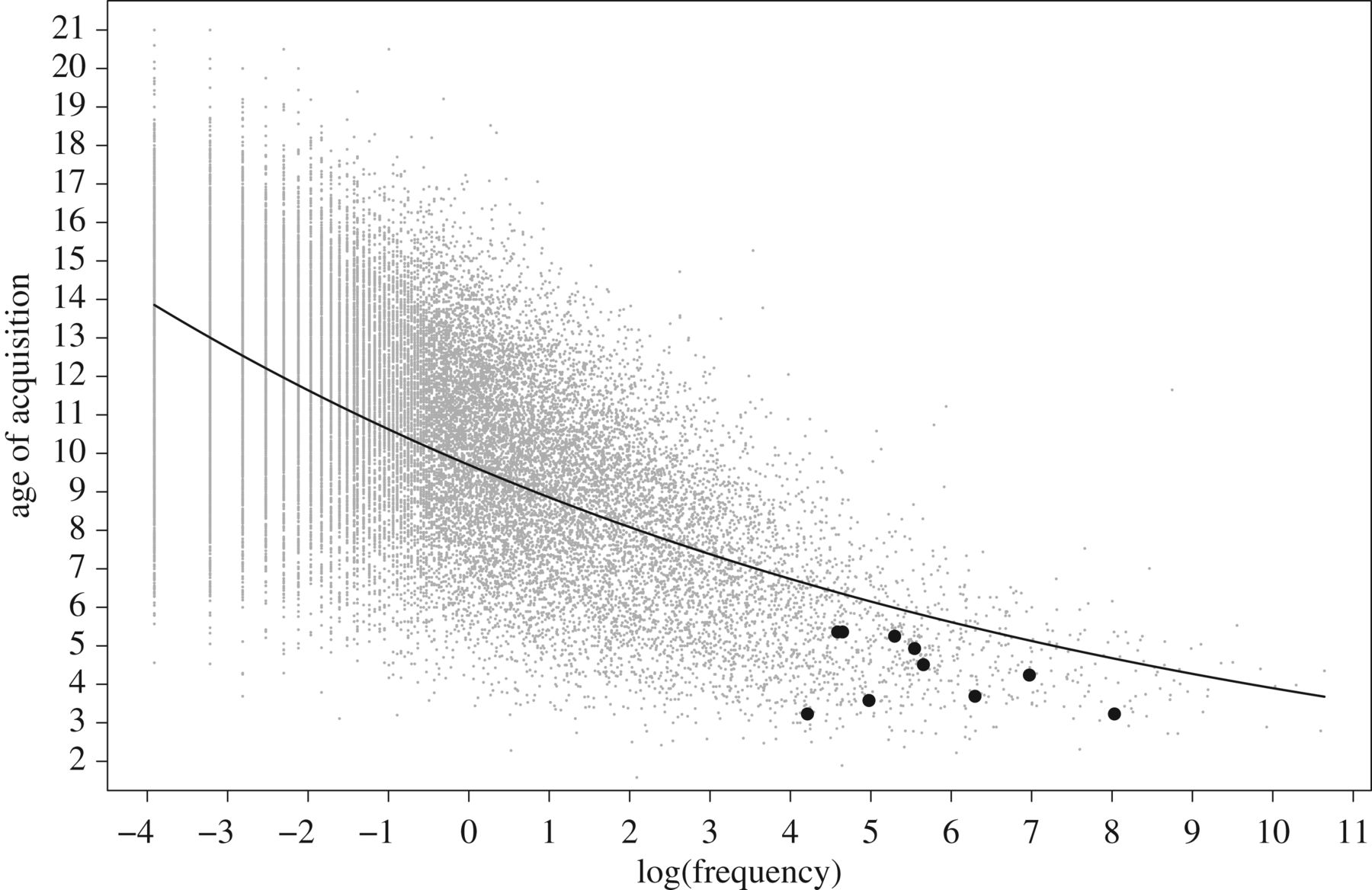
Dit wordt afgebeeld op de figuur hierboven. Er is (logischerwijs) een relatie tussen de frequentie waarmee een woord voorkomt en de leeftijd waarop een kind het leert: hoe frequenter een woord, hoe groter de kans dat een kind het op jonge leeftijd tegenkomt. Maar jonge kinderen leren de (lage) telwoorden veel sneller dan je op basis van alleen hun frequentie zou kunnen verwachten.
Rekenkunde
Het is wel jammer dat de auteurs geen taalkundigen zijn. Anders hadden ze misschien geweten dat telwoorden ook anderszins vaak uitzonderlijk zijn. In het Nederlands kunnen lange klinkers bijvoorbeeld nooit gevolgd worden door ingewikkelde groepen medeklinkers zoals lf (de enige medeklinkerclusters die zijn toegestaan na een lange klinker eindigen op een s en/of een t: paars, paard, koorts). De enige uitzondering is twaalf. In het Frans hebben sommige woorden een medeklinker die soms wel wordt uitgesproken en soms niet: wel voor een klinker (petit ami), niet voor een medeklinker (petit camerade) of aan het eind van een zin (il est petit). De uitzondering is dix waarvan de slotmedeklinker niet wordt uitgesproken voor een medeklinker (dix camerades) maar wel aan het eind van een zin (il y en a dix). Telwoorden zitten dus niet alleen in een nauwe fonetische ruimte, maar ook een enigszins bijzondere.
En er is natuurlijk nóg iets bijzonders aan telnamen, namelijk dat ze een systeempje op zichzelf vormen. Op een bepaald moment krijgt een Nederlands kind in de gaten dat hij vanaf eenenvijftig verder kan tellen zonder dat iemand hem nog uitlegt wat het volgende woord is (behalve dat er natuurlijk een paar hordes te nemen zijn zoals honderd en duizend). Met andere woorden vallen die combinaties niet te maken: enkele en vijftig is geen goed woord, al kun je best bedenken wat het betekent (een getal tussen de vijftig en de zestig). Het is alsof in ons hoofd, inderdaad, de rekenkunde een eigen plaatsje heeft gekregen, net een beetje los van de echte taal, met korte, eenduidige woorden die ook niet zo snel veranderen.
In het Italiaans kan due wel soms ‘enkele’ betekenen: fare due passi is ‘wandelen’.
Van zo’n stukje word ik blij.
De meeste telwoorden zijn relatief jong, dat speelt misschien ook mee. Voorgeletterde samenlevingen hebben toch geen woord voor twaalf of achthonderdvierendertig?
Verder zou je misschien kunnen zoeken naar hersenaandoeningen waarbij iemand opeens niet meer kan tellen, maar verder gewoon kan praten. Dan zou er een apart breingebied mee gemoeid moeten zijn. Hebben de onderzoekers dat gedaan?
Mijn leunstoelverklaring is dat je op telwoorden zeer streng gecorrigeerd wordt, gedurende een lange periode. Dat correctiegedrag straalt daarbij uit naar de uitspraak van het woord, ook bij het doorgeven naar de volgende generatie.
Woorden als 834 of zelfs 12 zijn niet in het onderzoek betrokken, het gaat over lage telwoorden, die vermoedelijk ook in ‘voorgeletterde samenlevingen’ voorkomen, zij het misschien niet in alle. Dat doet denk ik wel een beetje afbreuk aan de leunstoelverklaring, want er zijn geen aanwijzingen dat kinderen vaker op ‘vier’ worden gecorrigeerd dan op ‘hand’. Ik weet eigenlijk niet of er onderzoek is gedaan naar afasie op dit punt.
Ik dacht ook even aan de ‘voorgeletterde samenlevingen’ die mijn naamgenoot hierboven noemt. Inderdaad lijken sommige volkeren het zonder hoge getallen te kunnen doen. Het gaat dan vooral om jagers-verzamelaars die nooit een landbouwbestaan hebben gehad. Die gaan soms boven de twee al de mist in. Maar onze voorouders zijn al sinds mensenheugenis landbouwers. De Proto-Indo-Europese vormen van ‘negen’, ’twintig’ en zelfs ‘honderd’ konden moeiteloos worden gereconstrueerd. De Proto-Indo-Europeanen waren veehouders (ook woorden als ‘schaap’, ‘koe’ en ‘paard’ zijn zonder moeite terug te vinden), en moesten bijvoorbeeld hun schapen tellen.
De meest logische verklaring voor de onveranderlijkheid van telwoorden is de aard van hun betekenis. Die is exact en relatief waardenvrij. Gewone woorden veranderen van betekenis: homme ‘man’ komt van het Latijnse homo ‘mens (m/v/x)’, ons ooi is verwant aan het Latijnse ovis ‘schaap (m/v)’. Metaforen en andere beeldspraak doen ook hun werk: ons boom is verwant aan het Engelse beam ‘balk’. Ook kunnen woorden of woordbetekenissen verdwijnen door taboewerking (zeiken was ooit een normaal woord voor ‘plassen’, en betekende daarvoor weer ‘nat maken’ – vgl. to soak). Voor telwoorden geldt dat allemaal niet: ze raken niet gauw belast, ze lenen zich niet voor beeldspraak en een kleine betekenisverschuiving zou tot grote verwarring leiden.
Een interessante observatie: het zou kunnen dat de genoemde jagers-verzamelaarssamenlevingen, die minder met getallen werken, wel eerder getallen verwarren. Een aanhanger van de Nostratische hypothese meende de wortel *ḳUṭV te reconstrueren van derivaten die soms ‘vier’, soms ‘zes’ betekenen. Ik ben de eerste om toe te geven dat de Nostratische theorie erg controversieel is, en dat je met zo’n voorgesteld cognaat de schijn tegen hebt (“zo kun je alles wel aantonen”). Maar dat hij het überhaupt overweegt, vind ik interessant: het volk dat die taal gesproken moet hebben, moet nog niet aan landbouw hebben gedaan. Voor wie het interesseert: een link.
Ik geloof ook iet dat er op betalen strenger gecontroleerd wordt dan op andere woorden. Wel natuurlijk op ‘derde’ i.p.v. drilde (wat veel kinderen lang blijven zeggen). Ook zou het interessant zijn om ons tientallig stelsel (dat het mogelijk maakt 61c 3n 71 enz. te tellen) te vergelijken met volkeren die een ander telstelsel hebben. Daar lijkt me (maar ik weet daar niets van) een stuk moeilijker.. Ook leuk dank een aan ‘ajam ajam’ , meervoud, twee, een boel….). We kennen wel het verschijnsel dat een paar, zowel 2 , als een gering aantal kan betekenen. En denk ook aan ’tientallen’. Honderdtallen kan dan weer niet, dan zeg je ‘honderden”.
Het bovenstaande ‘betalen’ is een wijziging van mijn computer…. Moet natuurlijk zijn tellen.
En drilde = ‘driede’. Automatische spellingscontrole kan heel irritant wezen.
Grappig! Zo zie je maar: taal leren is niet simpelweg overnemen wat je hoort. Opvallend dat die biologen vinden dat kinderen telwoorden relatief snel leren. Ik vind eigenlijk dat het behoorlijk traag gaat, zeker bij de eerste vier in de rij. Doen ze jaren over, ondanks de training die kinderen op school krijgen, en ondanks twee punten die je noemt: zowel het systeem-in-systeem punt als de relatief strakke vorm-betekenisrelatie zou kinderen goeie cues kunnen geven om die dingen te leren. (Dat ze dergelijke signalen oppikken, blijkt bijvoorbeeld uit hoe ze rangtelwoorden leren – zo’n driede als de poster hierboven noemt, spreekt een frequentiebenadering misschien nog overtuigender tegen.)
Overigens vind ik de data uit de figuur best lastig te interpreteren: de leeftijd waarop iets verworven wordt, is niet bij kinderen gemeten, en een onderscheid tussen begrip en productie wordt niet gemaakt. Ze hebben gewoon aan een grote groep internettende volwassenen gevraagd op welke leeftijd ze denken een woord te hebben geleerd. (“AoA estimates are typically obtained by asking a group of participants to indicate the age at which they learned various words.”) In hun voordeel spreekt dat volwassenen kennelijk allemaal vergelijkbaar antwoorden, maar ik vind het toch niet helemaal lekker. Hoe ga je voor jezelf eigenlijk na wanneer je iets geleerd hebt? Bovendien weten we heel goed uit de ontwikkelingspsychologie dat kinderen de eerste vier telwoorden 1 voor 1 leren, in trage stapjes, en dat de rest daarna relatief snel volgt; dat is niet helemaal in overeenstemming met die grafiek. (De telwoorden zijn daarin niet precies gelabeld, maar zelfs met een beetje goeie wil kan je – op één na – niet goed raden wat wat is). Misschien ligt dat ook wel aan de frequentiedata: die gaan niet over aan kinderen gerichte taal. Logisch, want in dergelijke corpora in CHILDES komen telwoorden vrijwel niet voor, maar ik denk dat je op andere frequenties uitkomt als je op een school of kinderopvang opnames zou maken.(Ik denk evengoed niet dat frequentie hier, eh, ’telt’, maar toch.)
Maar terugkomend op de vraag in het artikel: ik denk dat de derde verklaring meer in de buurt komt, dus dat telwoorden weerbaar zijn tegen verandering omdat ze iets complexers doen in de hersenen dan man en slapen. Dat is dan zó moeilijk of belastend dat we dat het liefste maar 1x doen. Dat telproces is (misschien wel daarom) ook behoorlijk geautomatiseerd, en het is moeilijk om daar verandering in aan te brengen. Denk ook aan tellen en rekenen in een tweede taal: zelfs zeer gevorderde tweedetaalleerders vallen bij tellen en rekenen vaak terug op hun moedertaal, al lijken die telwoorden nog zo op elkaar. (Overigens is dat “1x labellen” misschien ook een deel van de verklaring voor waarom kinderen niet derde of second en third gewoon gelijk uit hun hoofd leren, maar daar via een omweg – driede, twoth, threeth – moeten komen, maar dat terzijde.)
Eersterangs bijdrage!
Ook grappig is dat je in het Frans 36 kan gebruiken om te zeggen “veel”, en dan het liefst van al in het bereik van een negatie: Il n’y a pas trente-six façons de faire ça” = Er zijn geen 36 manieren om dat te doen = Je kan dat eigenlijk maar op één manier doen.