Door Marc van Oostendorp

Sommige dingen hebben alle talen met elkaar gemeen terwijl eigenlijk niemand weet waarom. Het geldt onder andere voor de Wet van Zipf. Zodra je een verzameling taalmateriaal neemt van voldoende omvang, gaat dit aan deze statistische wet voldoen. Gerrit Bloothooft schreef bijvoorbeeld eerder dit jaar uitgebreid over het feit dat hij ook geldt voor het bestand van Nederlandse namen.

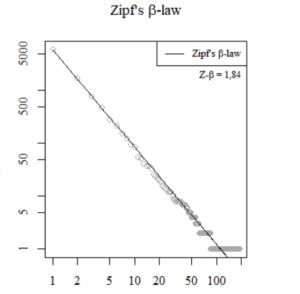
Wat is die wet ook weer? Je neemt een verzameling taalmateriaal van enige omvang – een roman, een verzameling gesproken woorden, alle jongensnamen die in een bepaald jaar gegeven worden – en zet ze op een rijtje. Op nummer 1 staat het woord of de naam die het vaakst voorkomt, op nummer 2 de naam die daarna het vaakst voorkomt, enzovoort. Vervolgens blijkt: woord 1 komt ongeveer twee keer zoveel voor als woord 2, dat weer ongeveer twee keer zo frequent is als woord 3, enzovoort. Wanneer je de woorden uittekent op een logaritmische schaal krijg je een rechte lijn – zoals hierboven wordt geïllustreerd aan de hand van de roman Karakter van Bordewijk.

Er zijn verschillende verklaringen voor de Wet van Zipf, In het proefschrift dat ze onlangs verdedigde in Utrecht stelt de taalkundige Marjolein van Egmond dat de meest waarschijnlijke iets te maken heeft met de opbouw van het menselijk geheugen, waar uiteindelijk alle woorden in worden opgeslagen. Dat deel van het geheugen, het ‘mentale lexicon’, is een netwerk. Als je een nieuw woord opslaat, leg je verbindingen met alle woorden die erin zitten, waarbij de verbindingen wat sterker zijn met woorden die bijvoorbeeld in vorm (lopen – kopen) of betekenis (lopen – wandelen) met elkaar te maken hebben. Maar dat betekent weer: hoe eerder je een woord opslaat, hoe meer verbindingen het in de loop van de tijd kan leggen. Recent geleerde woorden hebben maar weinig sterke verbindingen. Omdat je de frequentste woorden meestal het eerst leert (je hebt immers grotere kans dat je ze een keer tegenkomt), krijgen die dus uiteindelijk de meeste links. Wiskundige modellen laten zien dat een computer die op deze manier woorden leert, komt tot een verdeling die lijkt op de Wet van Zipf.

Dus wellicht is dat ook de manier waarop wij mensen woorden leren.

Om dat te onderzoeken, keek Van Egmond – onder andere – naar de taal van afatici, mensen die, doorgaans als gevolg van een hersenbloeding, een taalprobleem hebben gekregen. Ze nam opnamen van de spraak van zulke patiënten en zette ook daarin de woorden op een frequentielijst. Het Zipf-patroon kwam er weer keurig uit. Het zag er een beetje anders uit dan bij gezonde sprekers, maar dat had vooral te maken met een verklaarbaar verschil: afatici gebruikten minder verschillende woorden.

Volgens Van Egmond bewijst dit twee verschillende dingen tegelijkertijd. Aan de ene kant geeft het een steuntje aan de rug voor de verklaring van de Wet van Zipf uit de werking van het menselijk geheugen; aan de andere kant laat het zien dat het probleem van afatici niet is dat de structuur van hun mentale lexicon radicaal veranderd is. Alle woorden zitten er mogelijk zelfs nog in zoals voor de hersenbloeding; ze kunnen er alleen lastiger bij.