Voornamendrift (11) 

Door Gerrit Bloothooft

Hoe snel is zichtbaar dat een nieuwe voornaam populair gaat worden? Een indicatie zou de tijd kunnen zijn die het duurt voordat andere ouders de naam ook kiezen. Tot nu toe zijn er twee aanwijzingen dat die tijd kan variëren. Voor impopulaire namen die uiteindelijk in totaal maar twee keer gegeven werden is die imitatietijd gemiddeld langer dan voor alle overige nieuwe namen en op Britney reageerden ouders na “Baby One More Time” juist een stuk sneller. Eigenlijk dacht ik niet dat een latere populariteit al direct na het lanceren van een nieuwe naam zichtbaar zou zijn.  Maar ik had ongelijk.

Daarvoor duik ik eerst nog wat dieper in de ontwikkeling van een nieuwe naam, en bekijk de tijd tussen de eerste en de honderdste en vijfhonderdste naamgeving.  Het gaat weer om namen die tussen 1920 en 1960 voor het eerst zijn gegeven. Daarvan hebben 1.676 namen een frequentie van 100 en meer naamdragers terwijl  626 namen 500 keer en vaker zijn gegeven. Het is nog net voldoende om een kansverdeling te maken, zie figuur 1.

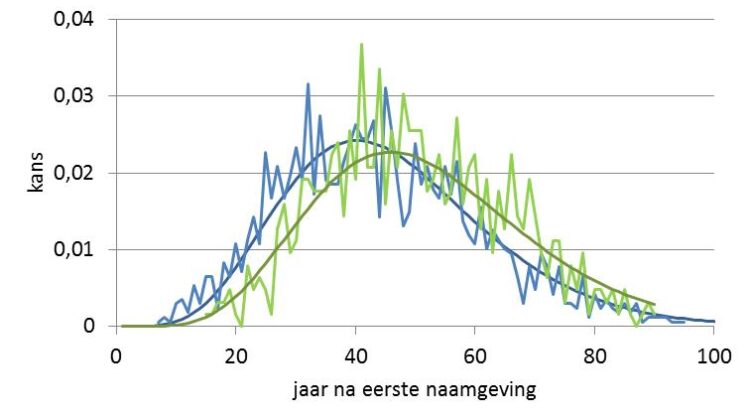
Als ik dit proces modelleer, dan blijken er respectievelijk 8 en 9 tussenstappen door sociale netwerken nodig te zijn tussen de eerste en 100^ste en 500^ste naamdrager. Voor de eerste 10 naamgevingen waren dat nog drie tussenstappen. Het verbaast natuurlijk niet dat er bij meer  naamgevingen meer sociale netwerken betrokken zijn. Maar ook de imitatietijd blijkt af te nemen. Was die voor de eerste 10 naamgevingen nog 12,8 jaar (mediaan), voor de 100ste en 500ste naamgeving is die nog maar 4,5 jaar.

Dat laatste gaf me te denken. Want ik ging er eerder vanuit dat de tijd tussen naamgevingen niet beïnvloed wordt door de namen die volgen. Die zijn immers nog helemaal niet gegeven. Maar misschien is die aanname niet juist en is er intrinsiek in een naam een potentie tot populariteit besloten omdat de naam voor die tijd net de juiste eigenschappen heeft.  Daarom ga ik terug naar de tijd tussen de eerste en de twee naamgeving en onderzoek die tijd nu als functie van de latere populariteit van de naam. Dat doe ik voor de namen die tweemalig blijven (en al eerder zijn besproken) en voor groepen namen die in totaal respectievelijk 3-10, 11-100, 101-500 en meer dan 500 naamdragers kregen. Het resultaat staat in figuur 2, in modellering met exponentieel dalende curven (met licht gekleurd erachter de gegevens zelf).

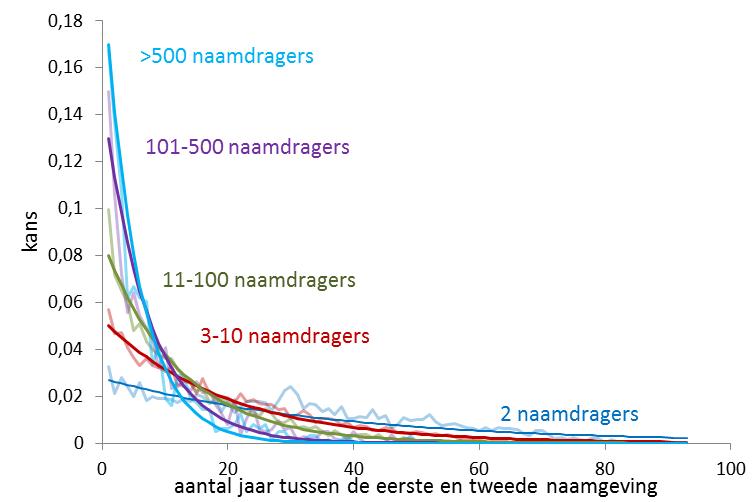
Het resultaat is verrassend duidelijk. De kans dat de eerste twee naamgevingen snel op elkaar volgen is voor later populaire namen aanzienlijk groter. De imitatietijd (mediaanwaarde) loopt terug  van 25 jaar (2 naamdragers) tot 3,7 jaar (>500 naamdragers). Hetzelfde zien we gebeuren in de tijd tussen de eerste en derde naamgeving in figuur 3.

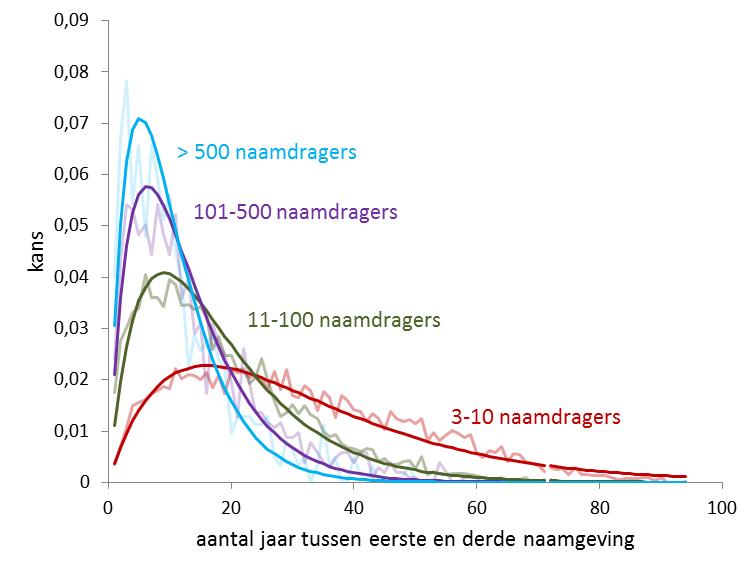
De modelleringen van de tijd tot de tweede en derde naamgeving hangt alleen maar af van de imitatietijd. Het lijkt erop dat die imitatietijd al in een naam besloten ligt, en het succes en uiteindelijk aantal naamdragers zal bepalen. Voor dat laatste is het aantal sociale netwerken dat de naam verder uitdraagt ook nog van belang, maar of dat een onafhankelijke factor is staat nog te bezien.

Het is verleidelijk om te denken dat wanneer populariteit zich al heel snel manifesteert, ruim voordat er grote aantallen naamdragers zijn, dit voorspellend gebruikt kan worden. Maar of we uit het tijdsverloop van de eerste naamgevingen de topnamen van de toekomst af kunnen leiden waag ik te betwijfelen, daarvoor is de statistische variatie waarschijnlijk veel te groot.

• Figuur 1: Benadering met respectievelijk p_1,9(j) en p_1,10(j) voor v = 0,15 (mediaan per stap is 4,5 jaar)
• Figuur 2: Benadering met de functie p_1,2(j) = v(1-v)^j-1 met voor n=2 , v=0,027 en mediaan 25 jaar;  n=3-10, v=0,05 en mediaan 13,5 jaar; n=11-100, v=0,08 en mediaan 8,3 jaar; n=101-500, v=0,13 en mediaan 5 jaar;  n>500, v=0,17 en mediaan 3,7 jaar. De mediaan van p_1,2(j) is ln(0,5)/ln(1-v).
• Figuur 3: Benadering met de functie p_1,3(j) = jv²(1-v)^j-1 met voor n=3-10, v=0,06; n=11-100, v=0,105; n=101-500, v=0,145 ;  n>500, v=0,175.