Voornamendrift (9)

Door Gerrit Bloothooft

Er wordt door ouders een voornaam bedacht die nooit eerder aan een kind in Nederland is gegeven. De naam spreekt andere ouders aan, en twee, drie, vier,…  tot misschien wel tienduizenden kinderen krijgen dezelfde naam. In de vorige aflevering liet ik zien dat de tweede naamgeving in hetzelfde jaar kan komen, maar ook wel 50 jaar op zich kan laten wachten. Voor de helft van de nieuwe voornamen komt de tweede naamgeving binnen 12,8  jaar. Als dat in dat tempo door zou gaan zouden we tot Sint Juttemis kunnen wachten tot een naam de top-10 bereikt. Er is ook wat anders aan de hand, en daarin spelen sociale netwerken een rol.

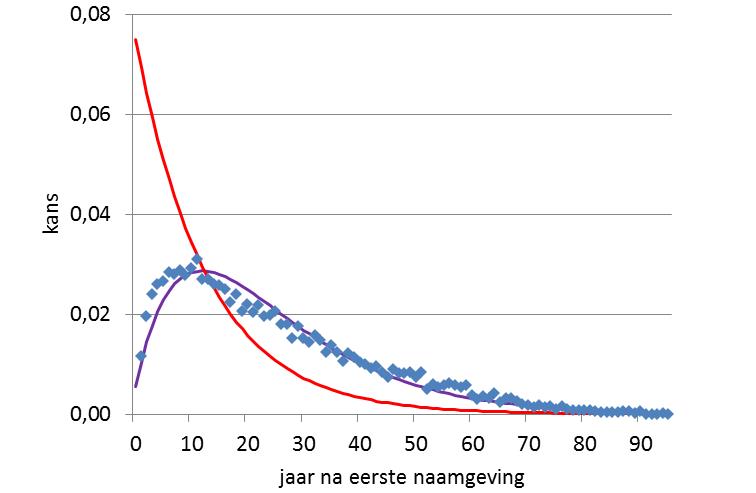
De tijd tussen de eerste en tweede naamgeving is bijzonder want dat is de enige keer dat we iets zouden kunnen zien van een directe beïnvloeding. Voor latere naamgevingen is het maar de vraag waarop of op wie ouders reageerden. De eerste naamgeving kan (naast een externe reden) de trigger zijn van alle volgende naamgevingen. Als dat zo is, dan zou je kunnen verwachten dat de tijd tussen de eerste en derde (en volgende) naamgeving precies zo verdeeld is als die tussen de eerste en de tweede.  Een andere optie is dat de derde naamgeving door de tweede is geïnspireerd, en de vierde door de derde, de vijfde door de vierde, enzovoort. Een kettingreactie van naamgevingen. Ik ga er daarbij vanuit dat de tijd tussen elke twee opeenvolgende naamgevingen op dezelfde manier verdeeld is als voor de eerste twee naamgevingen. Laten we dat toetsen voor de derde naamgeving (figuur 1).

Figuur 1. Verdeling van de tijd tussen de eerste en derde naamgeving voor 12.390 nieuwe namen die voor het eerst tussen 1920 en 1960 zijn gegeven. In rood de benadering van de kans voor twee opeenvolgende namen, in paars de theoretische curve als de namen op basis daarvan een sequentie vormen.

Het komt niet vaak voor dat de derde naam samen met de eerste en de tweede al binnen een jaar wordt gegeven. Dat doet vermoeden dat de derde naamgeving niet een reactie was op de eerste naam, maar op de tweede. Als er sprake is van een sequentie – dat de derde naamgeving een reactie is op de tweede (op dezelfde manier als de tweede een reactie is op de eerste) – dan zou in figuur 1 de paarse curve verwacht mogen worden. Dat lijkt er heel goed op.

Ik ga nu een stap verder en geef meteen de resultaten voor de tijd tussen de eerste en de vierde tot en met de tiende naamgeving. Dat geeft een onrustige lijnenwolk die evenwel goed begrensd is (figuur 2).

 

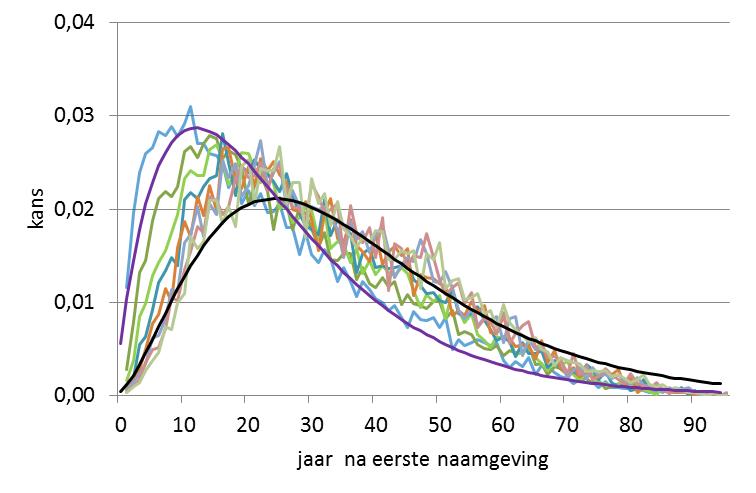
In figuur 2 is de paarse curve voor drie namen uit figuur 1 herhaald en is een zwarte curve toegevoegd die de theoretische kansverdeling voor een sequentie van vier namen geeft. Het resultaat is opmerkelijk. De resultaten van de derde tot en met de tiende naamgeving blijven zeer redelijk binnen de twee theoretische curven, en zijn te beschrijven als het resultaat van een weging van beide. Maar dat betekent dat de tiende naamgeving niet meer dan twee à drie tussenliggende naamgevingen van de eerste naamgeving af ligt. Dat suggereert dat een nieuwe naam zich in een beperkt aantal stappen via sociale netwerken zou kunnen verspreiden over heel Nederland. In figuur 3 wordt dat model afgebeeld.

 

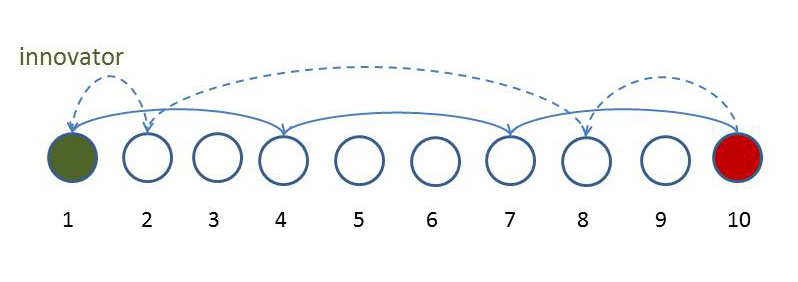
Dit doet sterk denken aan de theorie van ‘six degrees of separation‘, die stelt dat mensen slechts zes stappen verwijderd zijn van ieder ander op de wereld. Dan gaat het wel over recente verspreiding via sociale media en internet. Midden in de vorige eeuw was dat zonder internet zeker minder gemakkelijk, alhoewel ook toen al gedacht werd dat in Amerika het aantal stappen ongeveer drie zou zijn. Zo’n theorie is lastig te toetsen, maar het lijkt er op dat we het via naamgeving kunnen.

 

• De theoretische curves hebben de formules
  p_1,2(j) = v  * (1-v)^j-1
  p_1,3(j) = v² * (1-v)^j-1 * j
  p_1,4(j) = v³ * (1-v)^j-1 * j(j+1)/2

  In het algemeen geldt de recursie:
  p_1,k(j) = ∑ _t=1,j  p_1,k-1(t) * p_1,2(j-t+1)

  Dit kan nog elegant wordt herschreven als
  p_1,k(j) = v^k-1 * (1-v)^j-1 *c_k-1,j

  waarin  c_k-1,j getallen zijn uit de driehoek van Pascal (in rechthoekige vorm).

  De top van de verdeling valt in het jaar waarvoor geldt dat c_k-1,j/c_k-1,j+1 = 1-v

  Hier wordt v = 0,075 gebruikt. De top van de curve voor langere sequenties schuift dan steeds 12,8 jaar op (dat zien we in figuur 2 al bij 12,8 jaar voor k=3 en 25,6 jaar voor k=4). Voor k=10 zou dat 108 jaar zijn, wat duidelijk niet aan de orde is.