Voornamendrift (27)
Door Gerrit Bloothooft
 Nieuwe voornamen, ze beginnen allemaal met de eerste naamgeving. Een flink aantal blijft een eenmalige vondst van de ouders, andere worden nagevolgd, en een enkele naam wordt heel populair. Die aantallen liggen wonderlijk genoeg vast, in een Zipfiaanse verdeling. Een van de mooiste resultaten die ik in deze serie kon laten zien is dat die verdeling in de grond al in het eerste jaar van het bestaan van de nieuwe voornamen aanwezig is. Het is als het ontstaan van het heelal, in de oerknal ligt alles al besloten. Zo ook met voornamen. Maar als je het begin (een verzameling nieuwe voornamen) en einde (Zipfiaanse verdeling) kent, is dan ook de tussentijd te modelleren?
Nieuwe voornamen, ze beginnen allemaal met de eerste naamgeving. Een flink aantal blijft een eenmalige vondst van de ouders, andere worden nagevolgd, en een enkele naam wordt heel populair. Die aantallen liggen wonderlijk genoeg vast, in een Zipfiaanse verdeling. Een van de mooiste resultaten die ik in deze serie kon laten zien is dat die verdeling in de grond al in het eerste jaar van het bestaan van de nieuwe voornamen aanwezig is. Het is als het ontstaan van het heelal, in de oerknal ligt alles al besloten. Zo ook met voornamen. Maar als je het begin (een verzameling nieuwe voornamen) en einde (Zipfiaanse verdeling) kent, is dan ook de tussentijd te modelleren?
Ja, dat kan. Ik zal dat laten zien door voor de 29.756 nieuwe voornamen uit de periode 1920-1960 te berekenen hoe die zich de eerste jaren ontwikkelen. Daarvoor ga ik per jaar berekenen hoeveel namen er nog steeds uniek zijn, hoeveel er dan 2 naamdragers hebben, 3 naamdragers, etc. De aantallen zijn al bekend, want geteld en getoond in aflevering 16, en die kunnen als toets gebruikt worden. Deze aflevering biedt daarmee een synthese van allerlei stappen die eerder besproken zijn en die hier in samenhang voor modellering nodig zijn.
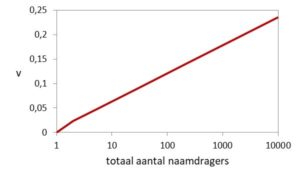
(kans op een naamgeving in een volgend jaar)
die nodig is om een totaal aantal naamdragers te bereiken.
Omdat het om modenamen gaat, is het uiteindelijk aantal naamdragers (f) eindig. En dat aantal bepaalt de verspreidingsfactor (v), de kans dat een naam in een volgend jaar ook door andere ouders wordt gekozen. Als een naam niet aanslaat is die nul en blijft de naam uniek, maar voor een succesvolle naam is de verspreidingsfactor hoog. De (gemiddelde) relatie tussen v en f staat in figuur 1 en is afgeleid uit een analyse van de tijd tussen de eerste en 2e, 3e etc naamgeving in aflevering 11. In formule is het v(f) = 0,063* log(f).
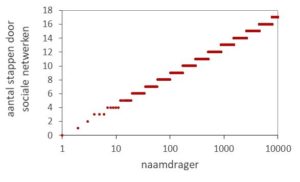
tussen de eerste en een latere naamdrager.
Een tweede aspect waar rekening mee gehouden moet worden is het aantal stappen (s) door sociale netwerken waarlangs een naam zich verspreidt. Hoeveel stappen er nodig zijn om vanaf de eerste naamgeving een latere naamdrager te bereiken staat in figuur 2, welke relatie ook weer is afgeleid uit de analyse in aflevering 11. In formule: s(f) = 4,2 * log(f).
De namen die binnen een stap worden gegeven hebben allemaal dezelfde kansverdeling van het aantal jaren (j) – ten opzichte van de eerste naamgeving – dat ze gegeven worden. Die kansverdeling kan worden uitgedrukt als ps(j,f), met s het aantal stappen, j de jaren, terwijl de verdeling ook nog afhankelijk is van f, het uiteindelijk aantal naamdragers (zie de toelichting onderaan).
Tenslotte moeten we weten hoeveel namen (n) er uiteindelijk een uiteindelijk aantal f naamdragers zullen hebben. Dat weten we uit de Zipfiaanse relatie: n(f) = n(1) / f α, met α = 1.56 is (zie aflevering 15) en n(1) het uiteindelijk aantal unieke namen. We weten hiermee hoeveel van de 29.756 namen er uiteindelijk uniek blijven, hoeveel namen 2 naamdragers zullen krijgen, hoeveel namen 3 naamdragers, etc.
Nu moet dit alles aan elkaar geknoopt worden om de ontwikkeling van de Zipfiaanse relatie te modelleren. Dat is een vrij ingewikkelde procedure die ik hier oversla, maar onderaan schets.
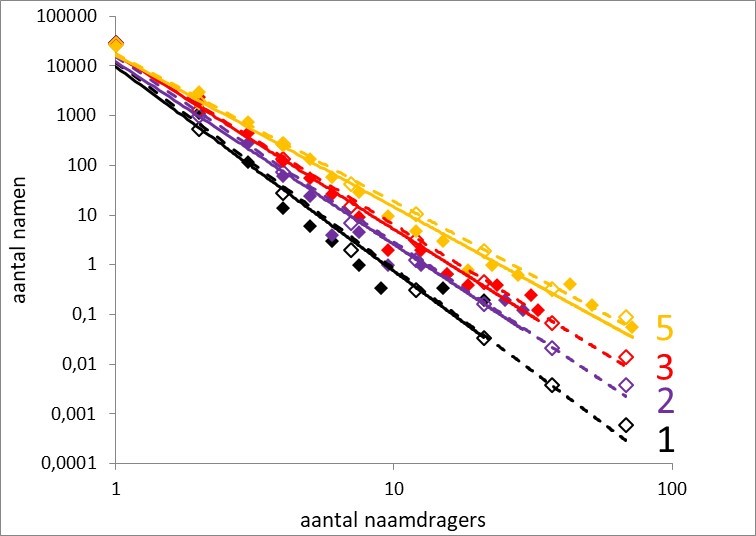
Het resultaat staat in figuur 3, voor de jaren 1, 2, 3 en 5. Er is een heel mooie overeenkomst met de werkelijke tellingen. Dat suggereert dat het model, waarin elke nieuwe naam intrinsiek eigenschappen heeft die de populariteitsontwikkeling ervan voorspellen, heel goed werkt. Die ontwikkeling kan worden beschreven met een verspreidings- of imitatiefactor en het aantal stappen door sociale netwerken, wat een plausibel mechanisme lijkt. Maar er zit nog wel een addertje onder het gras. Figuur 3 kon alleen worden bereikt met de verspreidingsfunctie v(f) = 0,040* log(f) in plaats van v(f) = 0,063* log(f) (zoals in figuur 1). Dat betekent dat de verspreidingssnelheid langzamer moet toenemen met de uiteindelijke frequentie dan ik eerder had afgeleid. Ik kan nog niet ontdekken wat daar de oorzaak van is, maar kom er nog op terug. Niettemin is de cirkel procedureel rond, waardoor de ontwikkeling van een Zipfiaanse verdeling verklaard kan worden uit de populariteitsontwikkeling van de onderliggende individuele namen. En dat is een prachtig resultaat.
- ps(j,f) is eerder omschreven als p1,k(j,f), zie aflevering 9 en aflevering 11.
p1,k stond daar voor de kansverdeling van de tijd tussen de 1e en ke naamgeving wat juist is voor de eerste naamgevingen, maar voor hogere naamgevingen niet. Dan telt het aantal stappen door sociale netwerken en dat wordt met ps beter uitgedrukt. Voor de volledigheid is de (recursieve) formule:
ps(j,f) = ∑ t=1,j ps-1(t,f) * p1(j-t+1,f) voor s>1 en p1(j,f) = v(f) * (1-v(f)) j-1 - Ik wil de ontwikkeling van de Zipfiaanse relatie vanaf het moment dat namen nieuw worden gegeven modelleren. Bijvoorbeeld in het eerste jaar na de innovatie: hoeveel namen blijven uniek, hoeveel namen hebben dan precies 2 naamdragers gekregen, hoeveel precies 3 naamdragers etc. Daarvoor moet je de kans weten dat de 2e (etc) naamdrager in jaar 1 geboren wordt, en voor hoeveel namen dat geldt. Voor de tweede naamdrager weten we bijvoorbeeld uit figuur 2 dat er precies 1 stap in een sociaal netwerk nodig is, en dat de kans daarop in jaar 1 dan ps(j,f) = p1(1,f) is. Om het aantal namen met twee naamdragers in jaar 1, n2(1), te weten moet deze kans met het aantal namen met uiteindelijk f naamdragers vermenigvuldigd worden en gesommeerd worden over alle mogelijke waarden van f: n2(1) = ∑ f = 2,fmax p1(1,f) * n(f). Voor de derde naamdrager zijn twee stappen in sociale netwerken nodig en geldt voor het aantal namen met drie naamdragers n3(1) = ∑ f = 3,fmax p2(1,f) * n(f). Voor hogere aantallen naamdragers moet aan de hand van s(f) = 4,2 * log(f) steeds vastgesteld worden hoeveel stappen gemaakt moeten worden om de juiste p functie te gebruiken. Deze procedure kan voor elk jaar j voor alle aantallen naamdragers worden uitgevoerd.Als dat gebeurd is moet nog een laatste correctie worden aangebracht. We berekenden namelijk bijvoorbeeld het aantal namen met een tweede naamdrager in jaar 1. Maar het is mogelijk dat ook de derde of volgende naamgeving al in het eerste jaar plaatsvonden. Om het aantal namen met precies twee naamdragers in jaar 1 vast te stellen moet het aantal namen die al drie of meer naamdragers in jaar 1 hebben eraf worden getrokken. En zo voor alle aantallen naamdragers.
Ik denk toch dat die parameter voor elke nieuwe naam weer varieert. Alleen zo kun de individuele verschillen in populariteit verklaren. Mohammed, Kemal, Britt en wie weet de nieuwste loot, Recep.
Klopt, er is spreiding. Weliswaar is v(f) een functie van het uiteindelijk aantal naamdragers f: v(f) = 0,040* log(f), maar bij een bepaalde f beschrijft dat een gemiddelde, waar ook nog een flinke variatie bij gevonden wordt. Maar om de Zipfiaanse ontwikkeling te verklaren volstaat die gemiddelde functie. Niettemin zoek ik in de aard van de spreiding de reden dat de coëfficiënt lager is dan ik had verwacht.