Voornamendrift (16) 

Door Gerrit Bloothooft

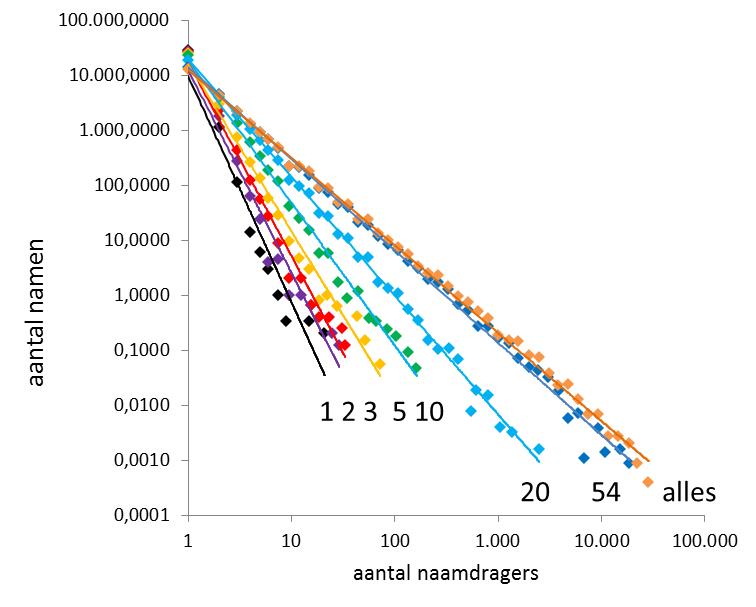
Figuur 1. Ontwikkeling van de Zipfiaanse verdeling voor 29.756 nieuwe voornamen uit de periode 1920-1960, voor 1, 2, 3, 5, 10, 20 en 54 jaar na introductie van een naam. Met ook het totale resultaat per 2014.

Ik moet bekennen dat ik na 15 afleveringen Voornamendrift nog geen verklaring voor de Zipfiaanse verdeling van voornamen heb gegeven, maar ik heb dat ook niet beloofd en ik weet niet of het gaat lukken. Wel liet ik zien dat die verdeling (van het aantal namen met een bepaald aantal naamdragers) te vinden is voor allerlei deelverzamelingen van voornamen, zoals namen voor mannen en vrouwen, namen per geboortedecade, en nieuwe namen uit de periode 1920-1960. Nu zijn die laatste namen bijzonder interessant want ze maken het mogelijk om het ontstaan van de Zipfiaanse verdeling te laten zien. Deze 29.756 namen zijn nieuw, want nooit voor 1920 gegeven (in ons bestand), en hebben zich minstens 54 jaar (tot 2014, ons selectiejaar) kunnen ontwikkelen. Daardoor kan ik laten zien hoe deze namen zich vanaf het startjaar uit het niets ontwikkelen tot een Zipfiaanse verdeling. En hoe lang dat duurt. Bij mijn weten is zo’n proces voor nog geen enkel ander domein eerder getoond.

Voor elke voornaam kan worden geteld hoeveel naamdragers er één jaar, twee jaar, drie jaar etc. na de introductie waren. Voor maximale precisie gebruik ik de geboortedatum van de eerste naamdrager waarna de volgende jaren ten opzichte van die datum worden vastgesteld. In het eerste jaar zullen de meeste namen nog maar één naamdrager hebben, een beperkt aantal twee, en nog veel minder meteen al drie of meer. Dat is de geboorte van een verdeling, die zelfs in jaar 1 al Zipfiaans blijkt te zijn, zie figuur 1 waarin de verdeling voor de jaren 1, 2, 3, 5, 10, 20, 54 na de introductie staat. Weliswaar zijn in het eerste jaar nog geen hoge aantallen naamdragers te verwachten en is de helling steil, er is toch al een goed passende lijn door de gegevens te trekken. Dat vind ik heel verrassend.

In jaar 1 is er zelfs een naam met meteen 21 naamdragers. Dat was in 1949 het geval met Mariandel  welke naam ongetwijfeld geïnspireerd is door het lied Kleine, blonde Mariandel, een vertaling van het Oostenrijkse lied Mariandl (1942). Het lied kreeg in 1949 in Nederland diverse vertolkingen waaronder die van Kees Pruis en gaf een vroeg media effectje, waarbij de naam – net zoals Britney – na een aantal jaren alweer vergeten was.

Kleine, blonde Mariandel
Wanneer gaan wij eens aan de wandel
Want steeds alleen te lopen
Is heus niets gedaan

Na het eerste jaar zullen 13.114 unieke namen nooit meer een naamdrager krijgen (althans tot 2014 blijft het bij één), maar de rest van de namen zal twee of meer keer gegeven worden. Dat kan zelfs voor de tweede naamgeving een flink aantal jaren duren wat we al eerder zagen voor tweemalige namen. In het algemeen daalt met de jaren het aantal namen dat nog één naamdrager heeft (van 28.461 tot uiteindelijk 13.144) en dat gaat ten gunste van het aantal verschillende namen bij hogere frequenties: dat aantal stijgt voortdurend met de tijd, maar steeds langzamer. Als gevolg daarvan draait de verdeling over de jaren naar een steeds vlakkere helling, die na ruim 50 jaar in de buurt komt van de uiteindelijke richting (hier gebaseerd op de telling in 2014 en in figuur 1 toegevoegd). Maar ze zijn allemaal Zipfiaans en kunnen samen met één formule, die nu afhankelijk is van het aantal jaren van ontwikkeling, worden beschreven: n(f,j) = n(1,j) * f ^α(j). Ik heb wel het gevoel dat het begrijpen hiervan steeds dichterbij komt.