Voornamendrift (18) 

Door Gerrit Bloothooft

We leren en leven door na te doen en zijn zelden origineel. Dat is misschien wel zo rustig want stel je voor dat we allemaal een unieke voornaam zouden hebben. Hoe we nadoen en kopiëren is trouwens boeiend genoeg. Het is de sleutel om te begrijpen hoe vernieuwingen breed navolging kunnen vinden, of juist niet. De kern van mijn eerdere betogen was dat wanneer ouders een kind een voornaam geven, dat een effect op anderen heeft. Die vormen de sociale omgeving in de breedste zin. Niet alleen familie en vrienden, maar ook buren, collega’s, andere ouders op school enzovoort. Als daar ouders bij zijn die een kind verwachten, dan zouden die het een mooie naam kunnen vinden en er ook voor kunnen kiezen. Bij nieuwe namen – ze worden toch wel eens geïntroduceerd –  is dat navolgingsproces goed te bestuderen. Ik dacht eerst dat zo’n proces niet van de nieuwe naam zou afhangen, maar vond dat voornamen die later populair blijken te worden al onmiddellijk na de introductie veel sneller nagevolgd worden. Dat ga ik hier verder uitwerken.

Ik haal in figuur 1 eerst een grafiek terug uit aflevering 8, waarin de kans staat hoe lang het duurt voordat een naam een tweede keer wordt gegeven (voor 16.516 nieuwe voornamen uit de periode 1920 en 1960 die tot 2014 minstens twee keer zijn gegeven). Deze kans neemt exponentieel af met de tijd. Er zijn namen die vrij snel overgenomen worden door andere ouders, maar ook (minder) namen waarbij het tientallen jaren kan duren. Op deze figuur kwam de reactie dat de benadering met zo’n  exponentiële functie niet zo goed was. Dat is juist en dat komt omdat de kans afhankelijk blijkt van de latere populariteit van de naam, en die differentiatie is in figuur 1 nog niet gemaakt. Ik beloofde dat goed te maken, en ga dat hier doen.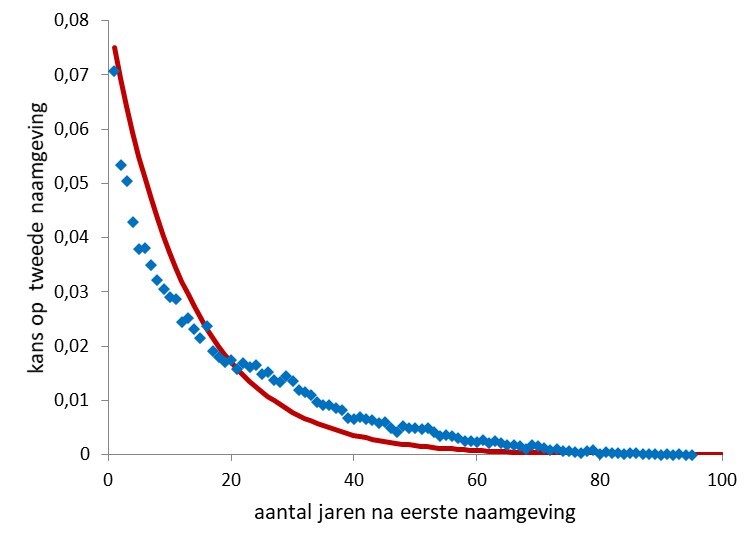

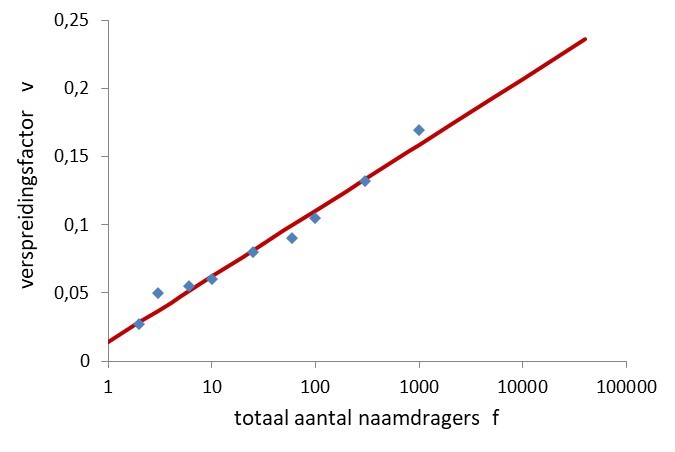
De benadering die in figuur 1 staat wordt helemaal bepaald door de kans dat een tweede naamgeving in het eerste jaar na introductie plaatsvindt. Dat noem ik de verspreidingsfactor v, en de exponentiële functie (rood) is p_1,2(j) = v (1-v) ^j-1, met voor het eerste jaar j=1 en p_1,2(j) = v = 0,075.  In aflevering 15 noemde ik al dat de factor v afhankelijk lijkt te zijn van het uiteindelijke aantal naamdragers f van een naam, dwz v(f).

 

In figuur 2 staan waarden voor v(f), die goed benaderd kunnen worden met de relatie v(f) = 0,021 ln(f) + 0,014. Figuur 2 zegt dat hoe populairder een voornaam is – of liever gezegd wordt – , hoe sneller de verspreiding zal gaan. Dat is intuïtief plausibel want anders haal je de grote aantallen niet in een beperkte tijd. De relatie is wel logaritmisch dus er is een steeds grotere toename  van de populariteit nodig voor eenzelfde toename van de verspreidingsfactor.

 

 

In figuur 1 zijn alle 16.516 verschillende voornamen gebruikt die meer dan één keer zijn gegeven. Die moeten onderscheiden worden naar het totaal aantal naamdragers:we moeten weten hoeveel verschillende namen n(f) er zijn met een bepaald totaal aantal naamdragers f.  Dat wordt nu juist door de Zipfiaanse relatie beschreven: n(f) = n(1) * f ^α,
met α = -1,57 (aflevering 15, wanneer de relatie is uitgekristalliseerd).

Alles bij elkaar wordt
p_1,2(j) = ∑ p_1,2(j,f) * n(f) = ∑ v(f) (1-v(f)) ^j-1 * n(1) * f ^α
met v(f) = 0,021 ln(f) + 0,014, terwijl de sommatie loopt over f = 2 tot f_max. Daarna wordt nog genormeerd zodat de totale kans 1 is.

De benadering in figuur 3 is uitstekend, alleen voor het 1^e jaar is de werkelijke kans op een tweede naamgeving hoger. Dit ondersteunt een populariteit-afhankelijk verspreidingsmodel. De gedachte is dat wat hier is aangetoond voor de tweede naamgeving, geldig is voor alle latere naamgevingen. Als een voornaam wordt geïntroduceerd is daar onmiddellijk een verspreidingspotentie aan gekoppeld, die verder ook niet meer zal veranderen. Dat wil zeggen dat alle ouders die hun kind bijvoorbeeld Noah noemen, of ze nu de eerste, tweede, tiende of duizendste naamgever zijn, eenzelfde effect op hun omgeving hebben waardoor een naam zich verder kan verspreiden. Maar hoe die intrinsieke potentiële populariteit van een voornaam ontstaat blijft vooralsnog wel een mysterie.

• Ik verwachtte dat voor een unieke naam v(1)=0 zou moeten worden, want er is geen verspreiding. Maar er is voor een goede benadering vanaf f=2 toch een kleine constante nodig.
• De waarden voor figuur 2 zijn afgeleid uit benaderingen voor p_1,k(j) [k=2,3,10,100,500] voor namen met 2, 3 tot 10, 11 tot 100, 101 tot 500, en meer dan 500 naamdragers, zie aflevering 11. De formule voor v(f) is iets preciezer dan die in de opmerkingen bij aflevering 15 wordt gegeven.
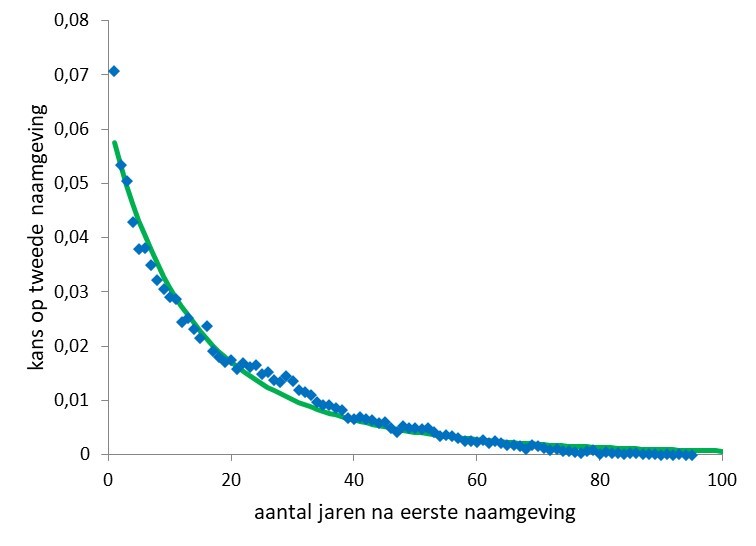
• De benadering in figuur 3 is gemaakt voor alle naamfrequenties tussen 2 en 1000.