Voornamendrift 104

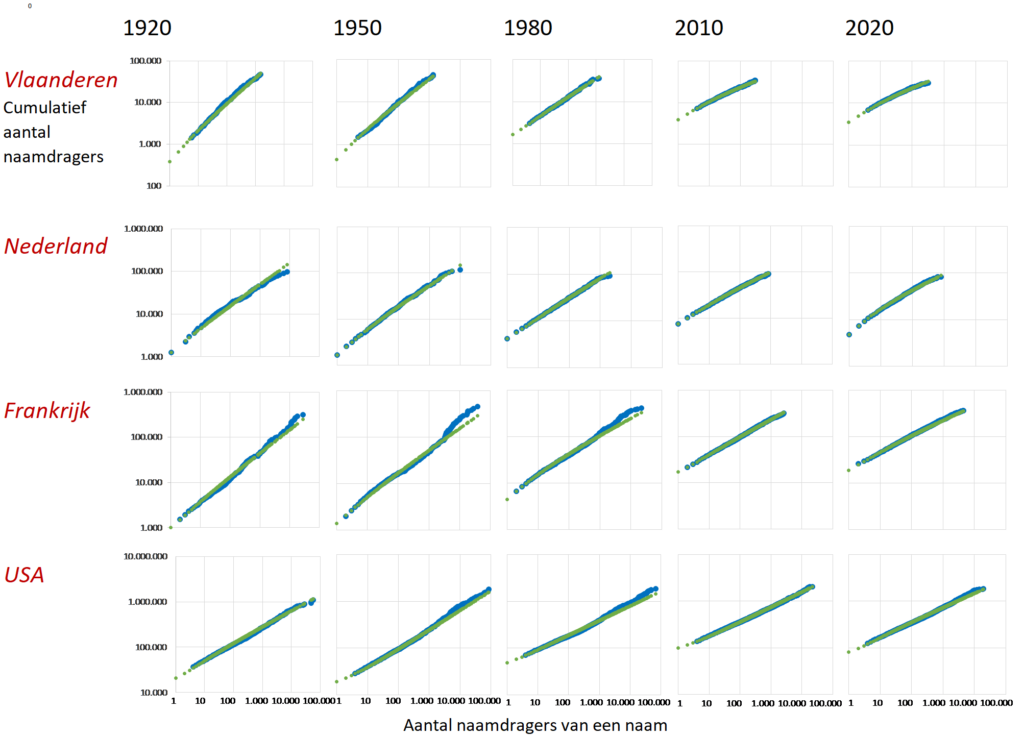
Er zijn verschillende manieren om de machtswet van voornamen te laten zien, maar die hierboven lijkt me grafisch de mooiste. Voor vier landen/gewest (Vlaanderen, Nederland, Frankrijk, USA) die spreiden in het aantal jaarlijkse geboortes van 40.000 tot 2 miljoen, en voor vijf jaren die een eeuw omspannen. In elke figuur wordt voor jongens cumulatief (het volgende bij het vorige optellen) het totaal aantal naamdragers gegeven, bij toenemende frequentie van de voornaam die ze dragen. We beginnen per land/jaar links met het aantal dragers van een unieke naam, en eindigen rechts met het optellen van de naamdragers met de populairste naam. Het verband is in alle gevallen vrijwel kaarsrecht op een dubbel logaritmische schaal, waarbij de blauwe punten de gemeten waarden zijn, en de groene punten de voorspelde waarden op basis van de best passende machtsrelatie.

Behalve dat opvalt hoe enorm goed de modelmatige voorspelling is, zien we dat de curve met de jaren in de vier landen afvlakt. Dat betekent dat er relatief meer laagfrequente en minder hoogfrequente namen zijn, de variatie in naamgeving neemt toe. Bovendien is te zien dat de populairste naam overal steeds minder naamdragers krijgt (in Nederland neemt dat aantal af van 8.322 jongens die in 1920 Johannes genoemd werden tot 669 jongens met de naam Sem in 2020): de curve wordt steeds korter.

Als alles opgeteld is, zijn we rechts in de grafiek aanbeland bij het totaal aantal gegeven namen, ofwel het totaal aantal geboorten in dat jaar. Dat is één van kengetallen die de getalsmatige eigenschappen van de voornaamgeving beschrijven. Die kengetallen zijn: (1) het aantal geboorten per jaar, (2) de exponent α uit de machtsrelatie n(f) = n(1) * f ^α , met n(f) als het aantal namen dat aan f kinderen is gegeven, (3) het aantal – unieke – voornamen n(1) dat wordt gegeven, (4) het aantal verschillende voornamen, en (5) het aantal kinderen dat de populairste voornaam krijgt. Het bijzondere is dat er  – door het bestaan van de machtswet – theoretisch maar drie kengetallen nodig zijn om de andere twee uit te rekenen.

Het bestaan van de machtsrelatie maakt voorspellingen mogelijk. Bijvoorbeeld dat de populairste voornaam minder naamdragers krijgt als gevolg van een toename van het aantal unieke namen (met andere factoren constant). Of dat het percentage unieke namen altijd tussen 35% en 50% van het totaal aantal verschillende voornamen ligt, en niet afhankelijk is van het totaal aantal geboorten maar alleen van α . In de praktijk is dat percentage zelfs hoger omdat een deel van de unieke namen zich aan de machtswet onttrekt.

Het is ook mogelijk om het kleinste aantal voornamen dat voldoende is om 80% van de kinderen een naam te geven uit drie kengetallen af te leiden. Dan kan begrepen worden onder welke omstandigheden dat aantal niet afhangt van het aantal geboorten per jaar. Dat was een verrassend eerder resultaat: dat bijvoorbeeld voor jongens dat aantal voor 1960 (100-200 namen) en ook nu (1300 namen) tussen Nederland en Amerika (USA) nauwelijks verschilt, terwijl het aantal geboorten in de USA twintig keer groter is. Daarover in de volgende bijdrage meer.

• Als de relatie tussen het aantal namen en naamfrequentie direct wordt weergegeven geeft dat een onduidelijk beeld omdat het minimaal aantal namen met een bepaalde frequentie alleen maar de gehele waarden 1 of 0 kan zijn, en geen waarde daar tussen. Dat kan enigszins opgelost worden door te middelen over logaritmische frequentie intervallen. Met de cumulatieve verdeling van het aantal naamdragers wordt dit allemaal vermeden. Het cumulatief aantal naamdragers stijgt monotoon met toenemende naamfrequentie.
• Uit de machtswet n(f) = n(1) * f ^α is de cumulatieve verdeling van het totaal aantal naamdragers af te leiden als
  cum(f) = n(1) *(1 + ((f+0,5) ^α+2  – 1,5 ^α+2)/(α+2) ) . Omdat bij hogere frequenties 0,5 ^α+2 genegeerd kan worden en door links en rechts de logaritme nemen krijgen we log(cum(f)) = (α+2) log(f+0,5) + constante, wat een rechte lijn in een log-log weergave oplevert, met positieve richtingscoëfficiënt α+2  (α heeft in de praktijk een waarde tussen -1,4 en -1,8).
• α valt uit de cumulatieve verdeling het beste af te leiden door α zo te kiezen dat het verschil tussen cum(f) en de gemeten waarden (kwadratisch) minimaal is. Maar zoals in de vorige bijdrage is besproken, zijn er vaak meer unieke voornamen dan de machtswet voorspelt: n(1)_gemeten = n(1)_model+ B.  Daarom moet niet alleen α maar gelijktijdig ook B zo gekozen worden dat het bovengenoemde verschil geminimaliseerd wordt.
• Voor Vlaanderen, Frankrijk en de USA worden uit privacy overwegingen de namen met de laagste frequenties niet beschikbaar gesteld. Door α en B voor de wèl beschikbare gegevens af te leiden kan, tezamen met het totaal aantal geboorten, voor de missende frequenties een schatting worden gemaakt, zoals in bovenstaande figuur te zien is (geen blauw, wel groen punt).
• Tussen het aantal unieke namen n(1) en het totaal aantal verschillende voornamen N bestaat de relatie N = n(1)*(1-1,5 ^α+1/(α+1)), die niet afhankelijk is van het aantal geboorten.
• In Nederland werden in 2010 in totaal 11.696 verschillende voornamen gegeven, waarvan 3.700 unieke namen “buiten” de machtswet. Dan resteren 7.996 voornamen “binnen” de machtswet waarvan er 3.873 uniek waren (48,4%), met α = -1,69. In totaal waren er 7.573 namen die één keer zijn gegeven, dat is maar liefst 65% van alle verschillende voornamen.
• Update 1-5-2023