De betekenis van woorden (3)

Zoals we al vaker hebben gezien ligt er veel wiskunde of logica aan de taal ten grondslag. Het duidelijkste zie je dat misschien nog wel bij woorden als iemand, niemand of iedereen. Op het eerste gezicht lijken die een heel duidelijke verwijzing te hebben. Iemand verwijst naar een enkele persoon, niemand naar geen persoon, en iedereen naar alle personen.

Maar dat is geen verwijzing in de letterlijke betekenis. Als een woord naar iets ver-wijst, betekent dit dat je datgene kunt aanwijzen. Als ik zeg dat Marie aan het slapen is of dat de slager een broodje eet, hoef ik alleen maar naar Marie of de slager te kijken om te controleren of de zin waar is. Maar als ik zeg dat niemand slaapt, moet ik van alle personen waar we het over hebben kijken of ze slapen of niet. Pas als geen van allen slaapt, is de zin Niemand slaapt waar. Net als dat we van al diegenen moeten zien of en zo ja wat ze eten, om uit te maken of de zin Iedereen eet een broodje waar is. En het volstaat ook niet om naar een bepaalde persoon te kijken of iemand slaapt. Om de juistheid van een zin als Iemand slaapt te bepalen, moet je alle relevante personen natrekken inzake hun activiteiten en pas stoppen zodra je een persoon vindt die slaapt. Woorden als iemand, niemand en iedereen kun je daarom niet begrijpen als een enkele verwijzing, terwijl dat wel geldt voor woorden als Marie of woordgroepen als de slager.

Dus moeten we terug naar de middelbare school – in ieder geval moet ik dat, want daar leerde ik wat wiskundige verzamelingen zijn. Verzamelingen zijn groepen met elementen die allemaal een bepaalde eigenschap delen. De verzameling even getallen bestaat bijvoorbeeld uit die getallen die je door twee kunt delen zonder op een half uit te komen. De verzameling slapers bestaat uit alle levende wezens die slapen.

Je kunt ook relaties tussen verschillende verzamelingen aangeven. De twee belangrijkste relaties die ik heb moeten leren zijn de doorsnede en de deelverzameling. De doorsnede van twee verzamelingen is de verzameling van elementen die tot beide verzamelingen behoren. De doorsnede van de verzameling slapers en de verzameling kinderen is de verzameling van slapende kinderen. De doorsnede van de verzameling van de even getallen en de verzameling getallen tussen 1 en 10, is de verzameling van elementen 2, 4, 6, 8 en 10.

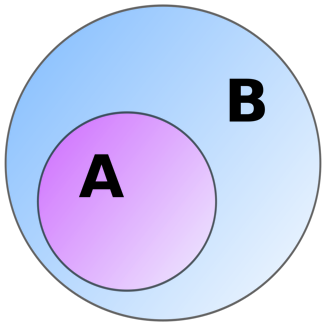
Deelverzamelingen zijn verzamelingen die deel uitmaken van een grotere verzameling. Bijvoorbeeld: de verzamelingen even getallen is een deelverzameling van de verzameling van alle getallen, en de verzameling kinderen is een deelverzameling van de verzameling mensen. Dat klinkt allemaal heel abstract, maar een tekening laat het heel makkelijk zien. In het linkerplaatje zie je in het rood de doorsnede van de twee witte verzamelingen; in het rechterplaatje is de paarse verzameling een deelverzameling van de blauwe verzameling.

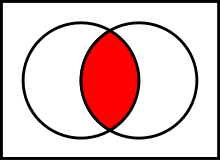
Waarom deze terugkeer naar de middelbare school? Het mooie is dat woorden als iemand, niemand en iedereen zich precies in termen van doorsnede en deelverzameling laten beschrijven. Iemand slaapt betekent dat de doorsnede van de verzameling mensen en de verzameling slapers gevuld is. Niemand slaapt zegt juist dat die doorsnede helemaal leeg is: er is geen mens die slaapt. En iedereen slaapt betekent dat de verzameling mensen een deelverzameling is van de verzameling slapers.

Woorden als iemand, niemand en iedereen zeggen dus iets over de relatie tussen de verzameling mensen en een andere verzameling: is de doorsnede daarvan leeg of niet, of is de verzameling mensen een deelverzameling van de andere verzameling?

En dan is het maar een kleine stap naar de meest basale kwantoren, zoals woorden als iemand, niemand en iedereen worden genoemd. Dat zijn de woorden een, geen en iedere (of alle). Een appel is groen betekent dat de doorsnede van de verzameling appels en groene dingen gevuld is. En Kim eet geen peer dat de doorsnede van de verzameling peren en de verzameling dingen die Kim eet helemaal leeg is. En iedere peer is groen of alle peren zijn groen betekent ten slotte dat de verzameling peren een deelverzameling van de verzameling groene dingen is.

Hoe dieper je in de taal duikt, hoe abstracter het wordt. Er is weinig wiskundigs aan een mooi gedicht of een ontroerend toneelstuk. Liefhebbers van taal hebben lang niet altijd iets met harde rekensommen. Maar de woorden waaruit die gedichten of toneelstukken bestaan zijn soms dezelfde woorden waar wiskundigen zich druk om maken. En u als lezer dus nu ook.

Op 2 november verschijnt van Hedde Zeijlstra het boek De betekenis van woorden, deel 1 in een reeks Het Nederlands van nu. Bestelinformatie bij de uitgever