In de loop der jaren hebben mijn vrouw en ik – beiden neerlandici – een aardige collectie literatuurgeschiedenissen bijeengebracht, waaronder de meerdelige klassiekers van Knuvelder, Kalff en Te Winkel. Ook de afzonderlijke delen van de Geschiedenis van de Nederlandse literatuur hebben we bij verschijning trouw aangeschaft. Hoeveel literatuurgeschiedenissen wij precies hebben, weet ik niet uit het hoofd. Vermoedelijk staan er in onze bibliotheek ongeveer tien. Ik had ook kunnen zeggen dat we er circa tien in de kast hebben staan. Hoe dan ook, het kunnen er een paar meer of een paar minder dan tien zijn.

Als er bij telling van ons boekenbezit acht of twaalf literatuurgeschiedenissen blijken te zijn, zou ongeveer of circa nog steeds een adequate omschrijving van ons bezit zijn. Een taalkundige zou zeggen: de woorden ongeveer en circa modificeren het telwoord in de nominale constituent.

Schattingsparen

Om aan te geven dat ik niet precies weet hoeveel literatuurgeschiedenissen we precies in ons bezit hebben, zou ik ook gebruik kunnen maken van wat de e-ANS schattingsparen noemt. Dat zijn uitdrukkingen waarbij twee opeenvolgende telwoorden worden genoemd:

• In onze bibliotheek staan een stuk of acht, negen literatuurgeschiedenissen.

Schattingsparen moeten volgens de e-ANS aan twee voorwaarden voldoen: het eerste getal moet kleiner zijn dan het tweede en beide getallen maken bij voorkeur deel uit van dezelfde rekenkundige reeks, waarin ze elkaar direct opvolgen. Als voorbeelden worden genoemd: 1, 2, 3 (stappen van 1), maar ook 5, 10, 15 (stappen van 5) en 10, 20, 30 (stappen van 10), enz.

In deze voorbeelden staan de telwoorden direct naast elkaar. Een andere mogelijkheid om een aantal te modificeren is door een schattingspaar te verbinden met het formele, aan het Frans ontleende voorzetsel à, dat geen ruimtelijke en geen temporele maar een andere relatie uitdrukt:

• In onze bibliotheek staan acht à negen literatuurgeschiedenissen.

Tusschenruimte

Volgens het Woordenboek der Nederlandsche Taal (WNT) doet het voorzetsel à dienst om een hoeveelheid als de laatste term van een reeks te kenmerken:

Het wordt gebezigd in uitdrukkingen, die strekken om de grootte eener hoeveelheid, die men niet geheel juist kan of wil opgeven, ten naaste bij te bepalen door de grenzen aan te wijzen, tusschen welke zij moeten gelegen zijn. 

In een opmerkelijke aanmerking bij dit uit 1882 daterende artikel uit het WNT wordt aan het gebruik van à wel een beperking opgelegd:

Daar a eene tusschenruimte tusschen twee uitersten onderstelt, kan het niet gebezigd worden bij twee onmiddellijk opeenvolgende hoeveelheden van ondeelbare voorwerpen. Men kan b.v. niet zeggen: zeven a acht personen, drie a vier schapen, elf a twaalf enkele guldens; men zegge: zeven of acht personen, drie of vier schapen, elf of twaalf guldens. Doch waar sprake is van grootheden, d.i. van deelbare dingen, als maten, gewichten, geldswaarde, tijd enz., kan a zeer gepast tusschen twee opeenvolgende getallen staan, vermits tusschen beide een gebroken getal kan bestaan, b.v. 7 a 8 pond, 3 a 4 mud, dat kost 11 a 12 gulden, dat zal 3 a 4 uren duren.

Het supplementdeel van het WNT stelt dat het bezwaar tegen het gebruik tussen twee onmiddellijk opeenvolgende hoeveelheden van ondeelbare voorwerpen over het algemeen niet gevoeld wordt door taalgebruikers. Wel is het zo dat à vaker wordt gekozen wanneer men wil aangeven dat het niet om een keuze gaat. Is dat wel het geval dan is of te verkiezen boven à.

Opkomst van à

Het voorzetsel à is ontleend aan het Frans en wordt in Nederland vanaf de 17^e eeuw gebruikt. In die periode komen ook de eerste Nederlandse kranten van de drukpers: op Delpher zijn 15.706 exemplaren verzameld, afkomstig uit verschillende binnen- en buitenlandse bibliotheken en archieven. Delpher is een geweldige krantenbak waar ik altijd met veel plezier in grasduin, maar voor (taalkundig) onderzoek is deze niet altijd even geschikt. Dat heeft deels te maken met OCR-fouten en deels met de gebrekkige tekstuele zoekmogelijkheden.  

Het Couranten Corpus, waarin een substantieel deel van de Nederlandstalige kranten uit Delpher is opgenomen, komt aan beide bezwaren tegemoet: de 17^e-eeuwse kranten zijn zorgvuldig overgetypt door enthousiaste vrijwilligers, voorzien van metadata en bovendien automatisch taalkundig verrijkt met lemma en woordsoort. Hierdoor is het mogelijk geworden om te onderzoeken of de regels waaraan een constructie met à tegenwoordig moet voldoen overeenstemmen met het gebruik van de constructie door 17^e-eeuwse journalisten.

Met de zoekbalk in Delpher is het onder andere vanwege de vele mogelijkheden praktisch ondoenlijk om deze à-constructies op te sporen. Met Geavanceerd zoeken in het Couranten Corpus daarentegen is dat niet bijzonder ingewikkeld. Kennis van Corpus Query Language is niet nodig, al is het wel handig als je een klein beetje vertrouwd bent met een beperkt aantal reguliere expressies; ik schreef daar eerder al eens over op Neerlandistiek. 

À-constructie

De à-constructie bestaat uit drie componenten: een getal, het voorzetsel à en een tweede getal. Voor elk van de delen kunnen we in Geavanceerd zoeken een eigen blok opstellen. Het eerste is een willekeurig getal van 1 cijfer (eenheden), 2 cijfers (tientallen), 3 cijfers (honderdtallen), 4 cijfers (duizendtallen), 5 cijfers (tienduizendtallen), enz. In principe kun je tot in het oneindige doorgaan maar in de praktijk zullen getallen boven de 100000 amper voorkomen in à-constructies. Ik beperk me hier daarom tot getallen van maximaal vijf cijfers, dus van 1 tot en met 99999.

Het tweede gedeelte bestaat uit het voorzetsel à. Het is verleidelijk om in dit blok à als lemma en niet als woord te selecteren. Toch is dat niet aan te raden. De accent grave werd namelijk lang niet altijd gebruikt; in de 17^e eeuw volstond een gewone a als voorzetsel. Het Couranten Corpus is automatisch gelemmatiseerd en van een woordsoort voorzien. Daarbij zijn niet alle a’s zonder accent herkend als het voorzetsel à. Om beide vormen te vinden, kun je dus het best van woordvormen uitgaan. Met een verticale streep – een pipe – geef je aan dat er gezocht moet worden naar de woorden a of à.

‘Regulier’ zoeken

Hoe kun je er nu voor zorgen dat je in het Couranten Corpus met één zoekopdracht alle mogelijke schattingsparen tot 100.000 vindt? Daarvoor maken we gebruik van twee soorten reguliere expressies. Met de eerste geven we aan dat we op zoek zijn naar een willekeurig getal uit de reeks van 0 tot en met 9. Dat doen we met [0-9]. Met de tweede geven we aan hoe vaak die reeks mag voorkomen. Hiervoor maken we gebruik van het vraagteken, dat aangeeft dat wat er direct voorstaat – in dit geval [0-9] – nul of één keer mag voorkomen.

Het is mogelijk om deze twee elementen te combineren tot [0-9][0-9]?[0-9]?[0-9]?[0-9]? Deze opdracht moet als volgt gelezen worden: zoek naar een willekeurig cijfer tussen 0 en 9 en herhaal dat een, twee, drie of vier keer. Daarbij geldt dat de laatste vier cijfers optioneel zijn. Zo kun je dus zoeken naar eenheden – het tweede, derde, vierde en vijfde cijfer komt niet voor – naar tientallen – het derde, vierde en vijfde cijfer komt niet voor – naar honderdtallen – het vierde en vijfde cijfer komt niet voor – naar duizendtallen – het vijfde cijfer komt niet voor – en naar tienduizendtallen – alle vijf cijfers komen voor.

De zoekopdracht ziet er – in Geavanceerd zoeken – dan als volgt uit:

Voor de liefhebber: vanuit Geavanceerd zoeken kun je deze zoekopdracht met één druk op de knop kopiëren naar Expert zoeken: [word=”[0-9][0-9]?[0-9]?[0-9]?[0-9]?”][word= “a|à”][word =”[0-9][0-9]?[0-9]?[0-9]?[0-9]?”]. Je kunt in deze zoekopdracht naar hartenlust elementen verwijderen, vervangen of toevoegen.

Onze zoekopdracht levert in totaal 11.544 resultaten op, verspreid over 503 groepen. Als we die vervolgens groeperen op annotatie (alle woorden in het resultaat op word) en daarna sorteren op alfabetische volgorde, dan zien we dat sommige resultaten naar alle waarschijnlijkheid geen schattingsparen zijn. Bijvoorbeeld wanneer het eerste getal groter is dan het tweede, zoals 100 a 50. Zo blijkt het in dit specifieke geval te gaan om prijzen van een loterij: er zijn honderd prijzen beschikbaar van (à) 50 gulden.

7 à 58

Een bijzondere constructie is die waarbij het eerste deel uit een enkel cijfer bestaat en het tweede deel uit een x-aantal tientallen +1, zoals 2 a 53, 6 a 27 en 8 a 49. Het zal duidelijk zijn dat tussen het eerste en het tweede getal geen verschil zit van 51, 21 respectievelijk 41 maar dat deze voorbeelden gelezen moeten worden als 52 à 53, 26 à 27 respectievelijk 48 à 49. Dit komt overeen met wat we in het huidige Nederlands wel zeggen maar niet meer schrijven. Ergens tussen de 17^e en de 21^e eeuw moet dit gebruik uit de geschreven taal verdwenen zijn. Hopelijk komen er in de toekomst ook 18^e– en 19^e-eeuwse kranten beschikbaar op basis waarvan we kunnen vaststellen wanneer dat gebeurd is.

eenheden

Het is geen eenvoudige opgave om de meer dan 11.000 gevallen van mogelijke schattingsparen te vergelijken. Om het onszelf gemakkelijk te maken splitsen we de grote zoekopdracht in enkele deelopdrachten. We beginnen met het zoeken naar schattingsparen die beginnen met een getal tussen de 0-9: [word = “[0-9]”] [word = “a|à”] [word = “[0-9][0-9]?”]. Dit levert 6009 gevallen op, bijna de helft van het totaal aantal voorkomens.

	+1	+2
0	0	0
1	75	1
2	1620	6
3	1242	5
4	704	22
5	722	1
6	338	111
7	341	3
8	175	468
9	119	1

Als we de gegevens uit de tweede en derde kolom verwerken in een grafiek dan levert dat het volgende resultaat op:

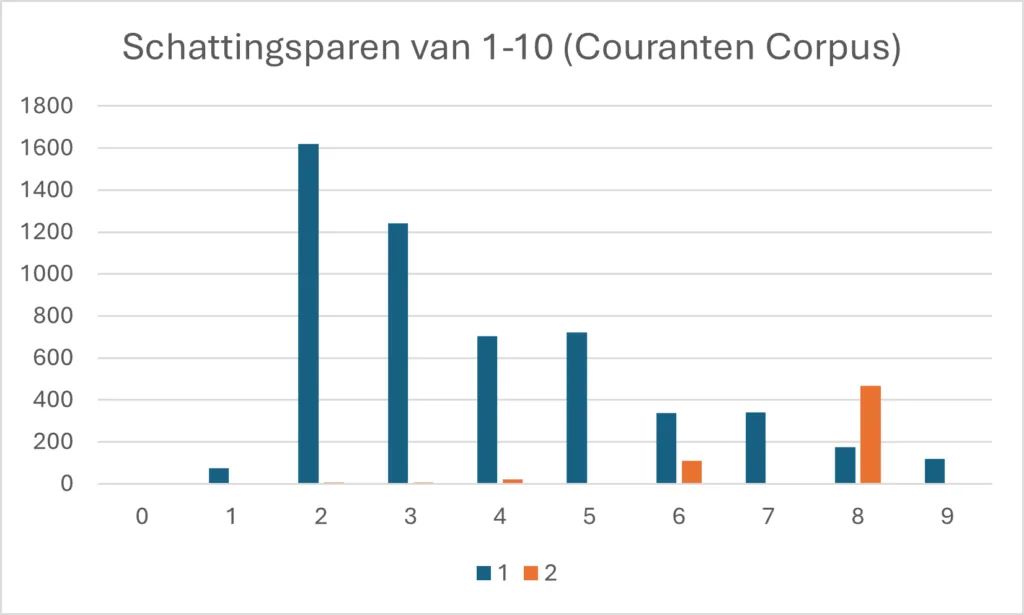
Uit de bovenstaande grafiek blijkt dat er een duidelijke voorkeur bestaat voor schattingsparen waarbij het verschil tussen de eenheden slechts 1 bedraagt. Een tweede conclusie is dat ‘lagere’ schattingsparen vaker voorkomen dan ‘hogere’. De schattingsparen 2 à 3 en 3 à 4 komen het vaakst voor. Ook 4 à 5 en 5 à 6 scoren hoog. Opmerkelijk genoeg komt 1 à 2 in het Couranten Corpus amper voor. (Misschien omdat je vaak in een oogopslag kunt zien of er sprake is van een of van twee dingen?) Bijzonder zijn de schattingsparen met 8: de uitdrukking 8 à 10 – met een stap van 2 – komt  bijna drie keer zo vaak voor als 8 à 9.  

tientallen

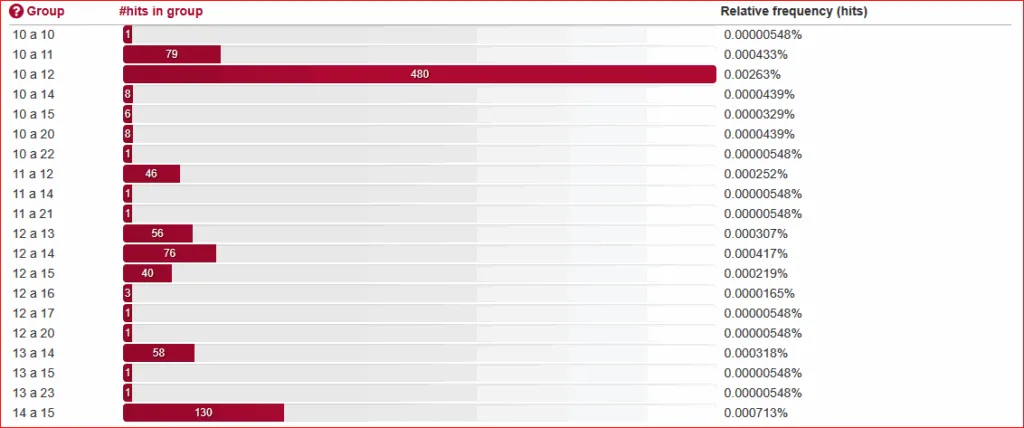
Ook bij schattingsparen waarbij het eerste getal tussen de 10 en de 20 ligt – 1476 gevallen in 41 groepen – bestaat een duidelijke voorkeur voor stapjes van 1 boven die van 2. Dat is te zien bij de getallen 11 (46x vs. 0x), 13 (58x vs. 1x), 14 (130x vs. 15), 15 (165x vs. 1x), 16 (62x vs. 43x), 17 (55x vs. 0x) en 19 (9x vs. 0x).  Daarentegen zijn stapjes van 2 populairder dan stapjes van 1 bij 10 (480x vs. 79x), 12 (76x vs. 56x) en 18 (53x vs. 24x).

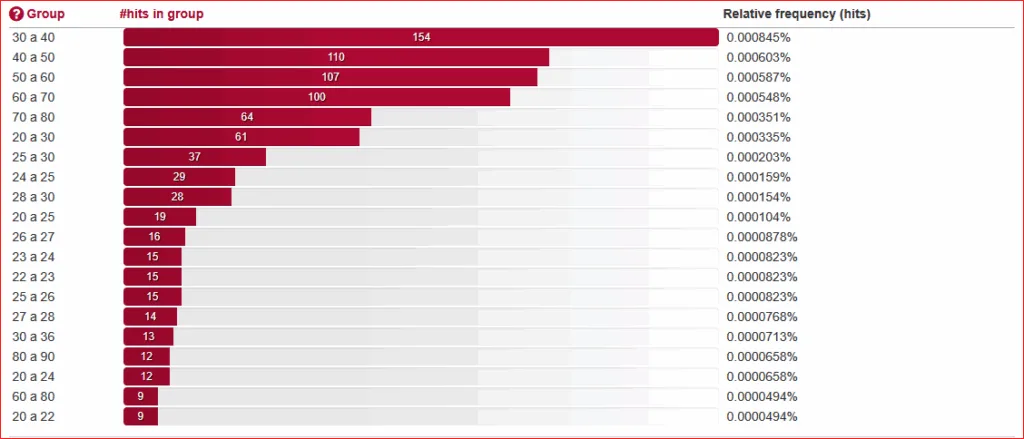
Van 20 tot 100 – 1129 resultaten verdeeld over 135 verschillende groepen – zijn stappen van 10 veruit het populairst. Alleen 90 à 100 valt met slechts 3 voorkomens uit de toon en is daarom ook niet te zien op de onderstaande schermafbeelding, met sortering op groepsgrootte.

honderdtallen

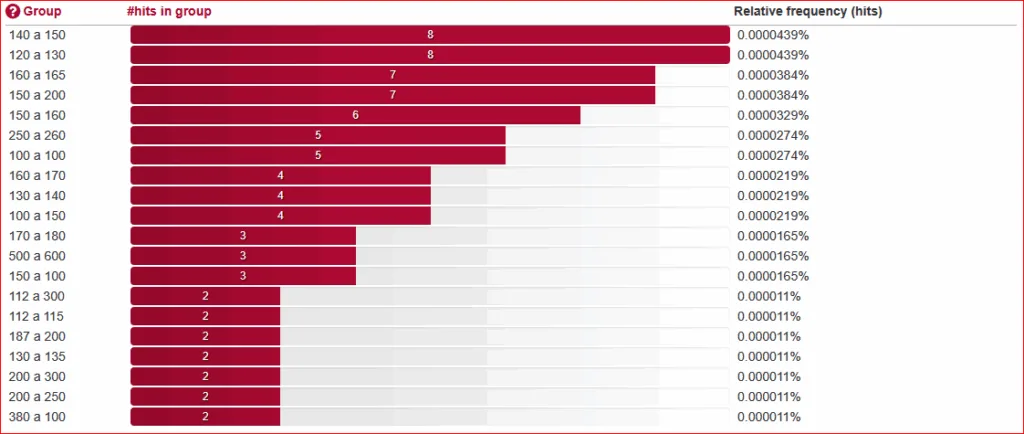
Van 100-1000 zijn er 115 paren verdeeld over 52 groepen. Daarvoor geldt dat paren met een verschil van 10 tussen linker- en rechtergetal het vaakst voorkomen. Ook stappen van 100 komen voor.  

(tien)duizendtallen

Schattingsparen met duizenden komen in het Couranten Corpus betrekkelijk vaak voor. Europa verkeerde in de 17^e eeuw geregeld in een staat van oorlog en de kranten maakten vaak melding van de grootte van een troepenmacht. Zo hadden de Turken in 1690 een leger van tussen de 70.000 en 80.000 man op de been gebracht.

Als we de resultaten van de schattingsparen met (tien)duizendtallen als laatste element sorteren op groepsgrootte, dan zien we dat stapjes van 1 het populairst zijn wanneer het eerste deel een getal onder de tien is, dus 5 à 6000. Stapjes van 2 komen in de top tien alleen voor bij 10 à 12000 en bij 8 à 10000.

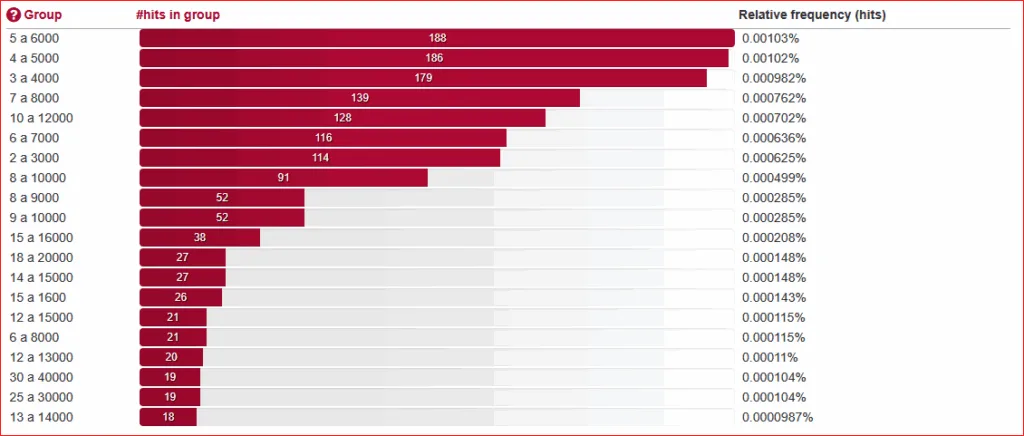
Uit nieuwsgierigheid heb ik in het Corpus Hedendaags Nederlands (CHN), een wekelijks groeiend corpus met voornamelijk kranten waarin trends in het Nederlands vanaf 2000 kunnen worden onderzocht, gekeken hoe vaak schattingsparen tot 10 daarin voorkomen. Alleen al voor die constructies levert dat corpus maar liefst 21.113 treffers op, verdeeld in 180 groepen. Als we slechts kijken naar de schattingsparen die 1 of 2 eenheden van elkaar afwijken, dan levert dat de volgende grafiek op:

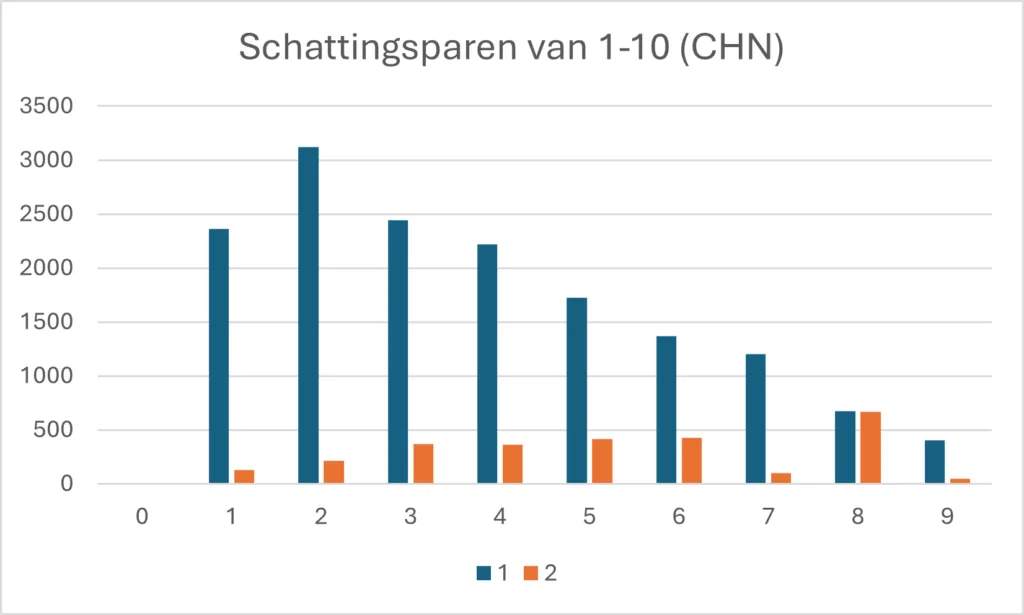
In essentie wijkt deze grafiek niet sterk af van die uit de 17^e eeuw. Ook hier zijn stapjes van 1 gebruikelijker dan stapjes van 2, komen lagere schattingsparen vaker voor dan hogere en neemt 8 ook hier een uitzonderlijke positie in. Wel zien we dat 1 à 2 veel vaker voorkomt dan in het Couranten Corpus. Zoals al eerder opgemerkt, ik zou ook graag de beschikking hebben over gemakkelijk doorzoekbare krantencorpora uit de 18^e, 19^e en 20^e eeuw.

Mijn schatting over het aantal literatuurgeschiedenissen in ons bezit, bleek trouwens tamelijk accuraat te zijn. Telling wees uit dat het er precies 8 zijn!